Zmienna losowa

Definicja

Funkcje 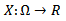nazywamy zmienną losową o wartościach w R, jeśli dla każdego a rzeczywistego zbior 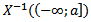jest zdarzeniem, czyli 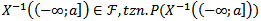jest określone.

Rozkład prawdopodobieństwa zmiennej losowej

Definicja

Rozkładem prawdopodobieństwa zmiennej losowej X nazywamy prawdopodobieństwo μ, określone na σ-ciele zbiorów borelowskich B(R) zależnością:

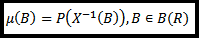
Rozkład dyskretny

Definicja

Zmienna losowa X ma rozkład dyskretny, jeśli istnieje taki zbiór przeliczalny SR, że μ(S)=1. Rozkład dyskretny daje się zapisać podobnie jak rozkład liczby oczek przy rzucie kostką. Wystarczy podać zbiór wartości S zmiennej losowej X i miary przypisane jego jednopunktowym podzbiorom.

Rozkład ciągły

Definicja

Mówimy, że zmienna losowa X jest ciągła (ma rozkład ciągły), jeżeli istnieje funkcja 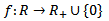, taka że:

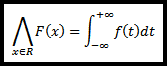
gdzie F jest dystrybuantą zmiennej losowej X. Funkcję f nazywamy funkcją gęstości prawdopodobieństwa (gęstością) zmiennej X.